Because of code confidentiality, this page only demonstrates the framework
PPM File Adjustment Algorithms
The primary image resizing algorithm is based on a seam-carving algorithm. The task of the algorithm set is to apply seam carving for content-aware resizing of images. The core algorithm works by finding and removing “seams” in the image that pass through the least important pixels. For a quick introduction, check out this video.
For example:

Table of Content
- Fundations of objects
- Basic functions and algorithms
- Examples of effects
- Potential improvement
1. Fundations of Objects
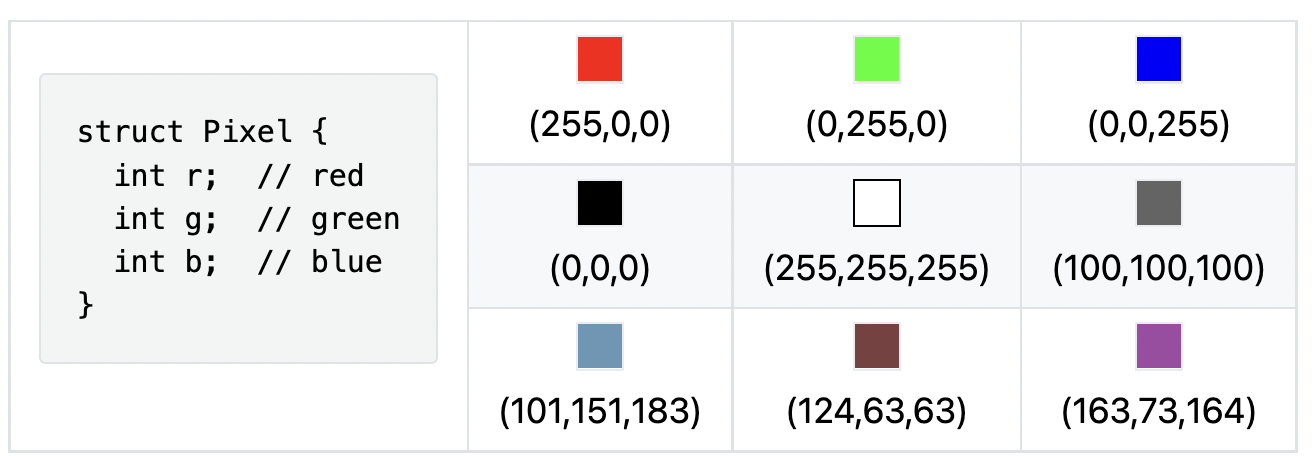
RGB Pixel
Each Pixel includes three integers, which represent red, green, and blue (RGB) color components. Each component takes on an intensity value between 0 and 255. The Pixel type is considered “Plain Old Data” (POD), which means it doesn’t have a separate object interface. Here is the Pixel struct and some examples:
RGB Image
An RGB image here is considered a matrix of RGB pixel(s). A matrix is a two-dimensional grid (grid[row_num][column_num]). Below is a 5x5 image and its conceptual representation as a grid of pixels:

PPM Format File
Here’s an example of an Image and its representation in PPM:
 However, to process color information more efficiently, each color’s channel is stored seperately.
The Image struct looks like this:
However, to process color information more efficiently, each color’s channel is stored seperately.
The Image struct looks like this:
struct Image {
int width;
int height;
Matrix red_channel;
Matrix green_channel;
Matrix blue_channel;
};2. Basic Functions and Algorithms
(1) Read in and save
Read in PPM Format files correctly, and create the corresponding dynamic objects.
(2) Rotate and resize images
(3) Processing: The seam carving algorithm
The seam carving algorithm works by removing seams that pass through the "least important" pixels in an image. We use a pixel’s energy as a measure of its importance.
To compute a pixel’s energy, we look at its neighbors. We’ll call them N (north), S (south), E (east), and W (west) based on their direction from the pixel in question (we’ll call it X).
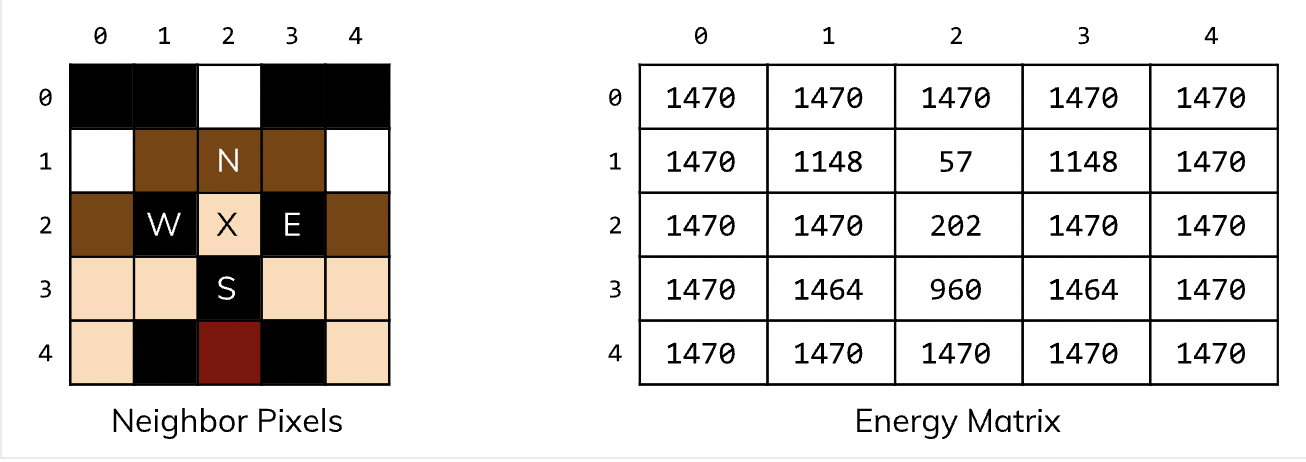 The energy of X is the sum of the squared differences between its N/S and E/W neighbors:
The energy of X is the sum of the squared differences between its N/S and E/W neighbors:
energy(X) = squared_difference(N, S) + squared_difference(W, E)We do a in-depth search. First we read in a new pixel, record the energy(X). When we find a new pixel each time we read, we put it in the searcing container. The search process should follow a "first in first out" rele.
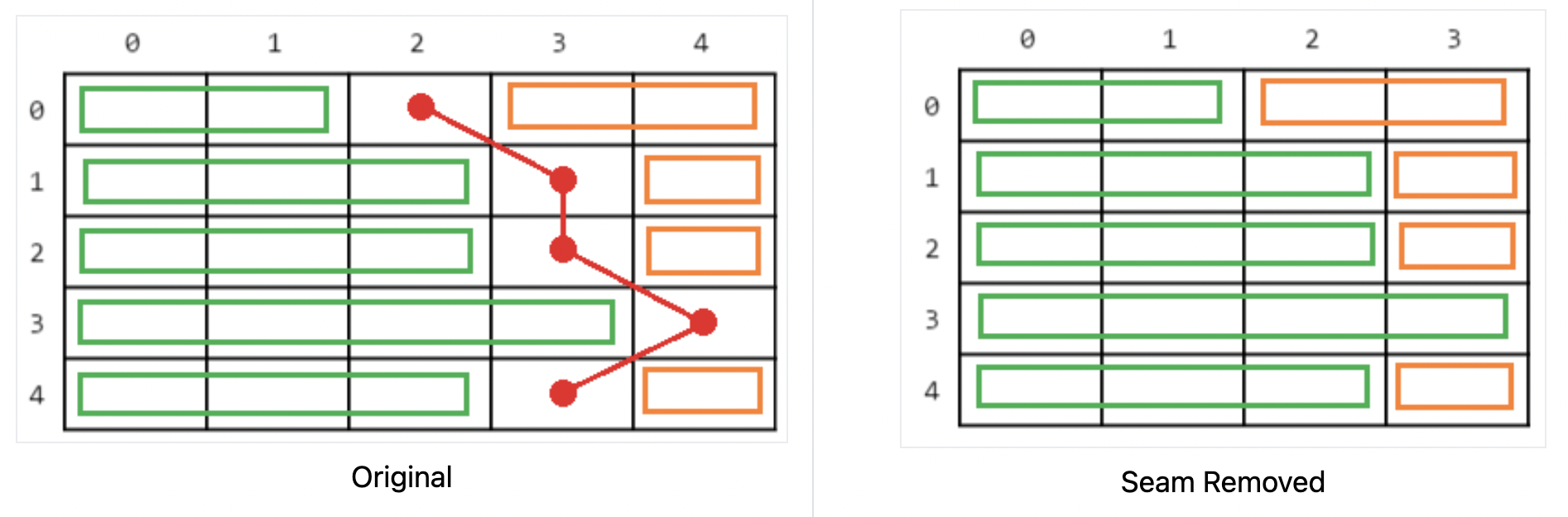
Once the energy matrix has been computed, the next step is to find the path from top to bottom (i.e. a vertical seam) that passes through the pixels with the lowest total energy (this is the seam that we would like to remove).We would want to choose the least costly from those pixels, which means the minimum cost to get to a pixel is its own energy plus the minimum cost for any pixel above it. This is a recurrence relation. For a pixel with row r and column c, the cost is:
cost(row, column) = energy(row, column) + min(cost(row-1, column-1),
cost(row-1, column),
cost(row-1, column+1))The seam array passed into this function contains the column numbers of the pixels that should be removed in each row, in order from the top to bottom rows. To remove the seam, copy the image one row at a time, first copying the part of the row before the seam (green), skipping that pixel, and then copying the rest (orange).
3. Examples of Effects
Small Example: dog
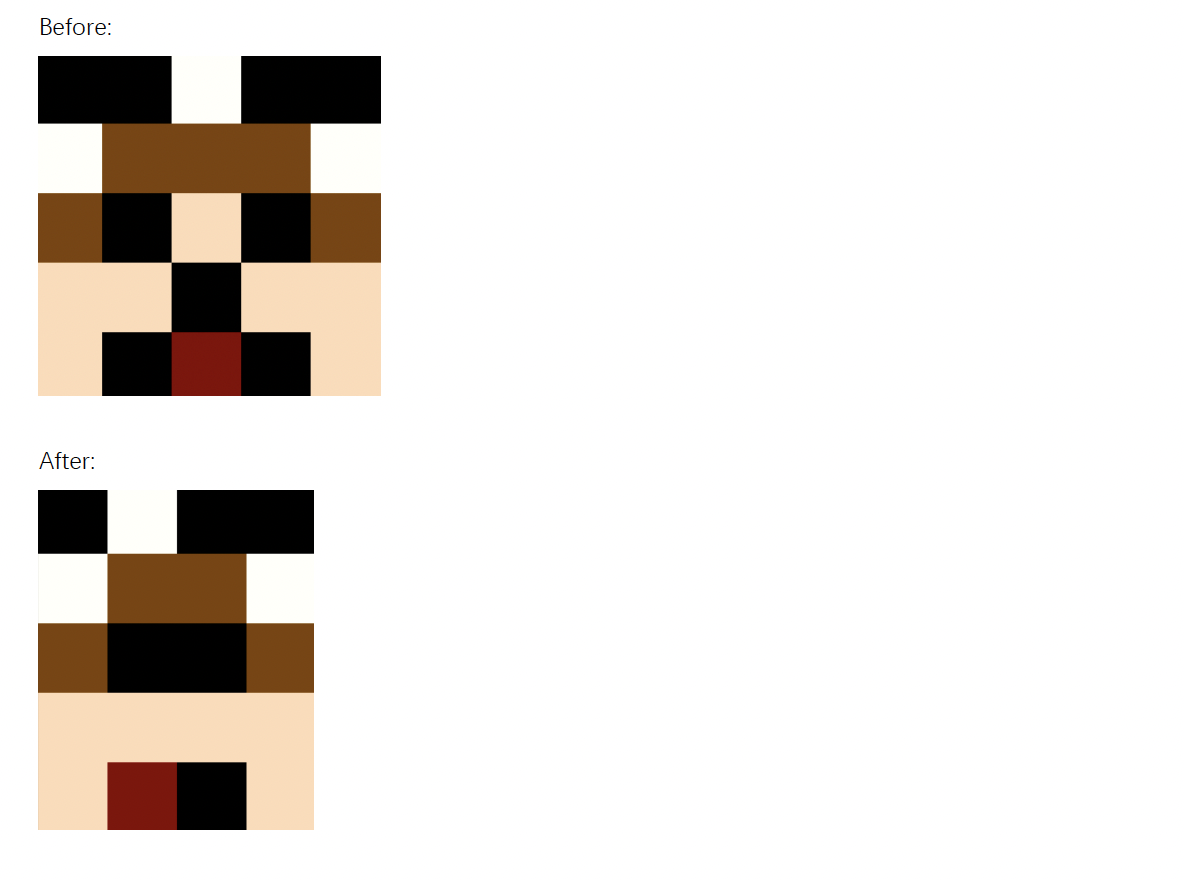
Small Example: crab


Medium Example: hourses


4. Potential Improvement
- Generate the energy matrices through searching the original and roated images
- remove pixels based on relative energy